Nowadays, mobile robots are being widely applied in various fields such as indoor carrying and check of products and outdoor exploration. One of the most important problems arising in development of mobile robots is to resolve path planning problem. With active studies of implementation of path planning, lots of algorithms have been developed and especially, the dramatic advance in artificial intelligence (AI) led to advent of algorithms using reinforcement learning (RL). Deep reinforcement learning (DRL) has been developed and it uses neural network to approximate parameters of RL algorithm. DDPG is one of deep reinforcement learning (RL) algorithms and is widely used to solve lots of practical issues as it doesn’t need full information of the environment. In other words, path planning with DRL has advantages of possibility for unknown environments in which partial or full information is not given and of direct controllability of the robot. Generally, path planning Up to now, path planning using DRL has considered only position control problem with no consideration of its orientation angle (as the author knows). In this paper, a pose control method using DRL for 3-wheeled omnidirectional mobile robot is proposed. And a method to reduce position error is mentioned. Simulation results show that the proposed method can efficiently solve the control problem of omnidirectional robots.
| Published in | International Journal of Industrial and Manufacturing Systems Engineering (Volume 10, Issue 2) |
| DOI | 10.11648/j.ijimse.20251002.12 |
| Page(s) | 36-43 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
3-wheeled Omnidirectional Mobile Robot, Deep Reinforcement Learning (DRL), DDPG Algorithm, Path Planning, Pose Control
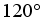 spacing and each wheel is an omnidirectional wheel.
spacing and each wheel is an omnidirectional wheel. 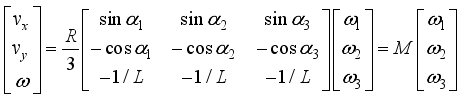 (1)
(1) 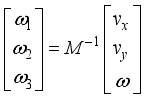 (2)
(2) 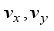 are linear velocity to x- and y-axis, respectively,
are linear velocity to x- and y-axis, respectively, 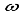 is angular velocity of the robot,
is angular velocity of the robot, 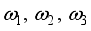 are angular velocity of each wheel,
are angular velocity of each wheel, 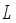 is radius of the robot body,
is radius of the robot body, 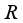 is radius of the wheel,
is radius of the wheel, 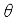 is orientation of the robot in absolute coordinate system and
is orientation of the robot in absolute coordinate system and 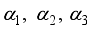 are angle of placement of each wheel.
are angle of placement of each wheel. 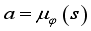 to take in that state, and the critic network computes the value
to take in that state, and the critic network computes the value 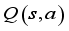 according to the action taken in that state. Repeating this process several times, we store the transition information in the experience repository. Then,
according to the action taken in that state. Repeating this process several times, we store the transition information in the experience repository. Then, 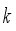 data are randomly extracted from the experience repository to train the network. The block diagram of the DDPG algorithm is shown in Figure 2.
data are randomly extracted from the experience repository to train the network. The block diagram of the DDPG algorithm is shown in Figure 2. 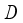 .
. 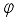 , critic network
, critic network 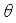 , target actor network
, target actor network 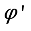 and target critic network
and target critic network 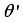 .
. 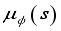 , choose action
, choose action 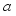 and add noise to search for new behavior.
and add noise to search for new behavior. 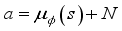
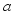 and move to the next state
and move to the next state 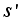 . Then, receive a reward
. Then, receive a reward 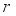 and save transition information in experience store
and save transition information in experience store 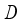 .
. 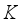 transition information in
transition information in 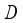 .
. 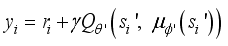
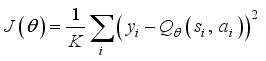
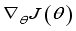 and update critic network using gradient descent method.
and update critic network using gradient descent method. 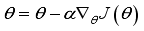
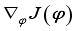 and update actor network using gradient ascent method.
and update actor network using gradient ascent method. 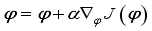
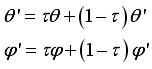
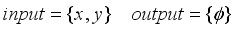 (3)
(3) 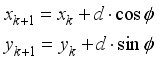 (4)
(4) 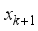 and
and 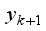 is position coordinates of the robot at
is position coordinates of the robot at 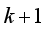 step,
step, 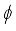 is output of actor network of DDPG: orientation angle of the robot and
is output of actor network of DDPG: orientation angle of the robot and 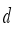 is length of movement of robot in one step (during sampling time).
is length of movement of robot in one step (during sampling time). 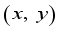 , but also the orientation angle
, but also the orientation angle 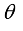 of the robot is considered as its state like Eq. (5).
of the robot is considered as its state like Eq. (5). 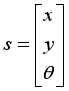 (5)
(5) 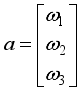 (6)
(6) 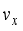 , y-axis velocity
, y-axis velocity 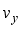 and the angular velocity of the robot body are calculated with its kinetic model and state of the robot can be updated by Eq. (7) from calculation of displacement and rotation angle during
and the angular velocity of the robot body are calculated with its kinetic model and state of the robot can be updated by Eq. (7) from calculation of displacement and rotation angle during 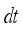 .
. 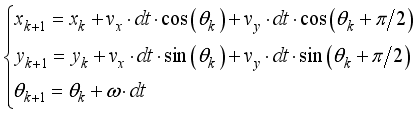 (7)
(7) 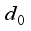 ).
).  (8)
(8) 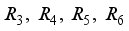 are calculated with Eq. (9).
are calculated with Eq. (9). 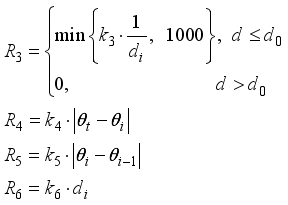 (9)
(9) 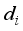 - Distance between robot and target at step
- Distance between robot and target at step 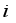
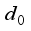 - Critical distance to estimate arrival to target region
- Critical distance to estimate arrival to target region 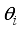 - Orientation of the robot at step
- Orientation of the robot at step 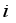
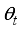 - Target orientation angle
- Target orientation angle 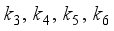 - Coefficients
- Coefficients 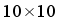 , the initial state of the robot is
, the initial state of the robot is 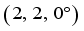 , the target state is
, the target state is 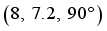 and 4 obstacles are placed randomly. The diameters of the obstacles are in range of
and 4 obstacles are placed randomly. The diameters of the obstacles are in range of 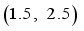 .
. Layer | Type | Number of parameters | Activation |
|---|---|---|---|
Input | 3 | ||
Layer1 | Dense | 32 | |
Layer2 | Dense | 256 | |
Layer3 | Dense | 32 | |
Output | Dense | 6 |
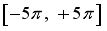 , so activation function of the output layer is set as
, so activation function of the output layer is set as 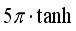 .
. Layer | Type | Number of parameters | Activation |
|---|---|---|---|
Input | 6 | ||
Layer1 | Dense | 32 | |
Layer2 | Dense | 256 | |
Layer3 | Dense | 32 | |
Output | Dense | 1 |
Parameter | Definition | Value |
|---|---|---|
Initial number of steps | 500 | |
Size of minibatch | 64 | |
Exploration noise | 0.5 | |
Updating frequency of the target network | 1 | |
Size of experience pool | 10000 | |
Learning rate | actor-10-4, critic-10-3 | |
Discount factor | 0.9 | |
Soft replacement factor | 0.001 |
Parameter | Definition | Value |
|---|---|---|
Negative reward when collide with obstacles | -1000 | |
Negative reward when depart from the map | -1000 | |
Coefficient | 10 | |
Coefficient | 5 | |
Coefficient | 20 | |
Coefficient | 3 | |
Radius of target region | 0.5 |
No | Previous algorithm | Proposed algorithm |
|---|---|---|
1 | 0.413808 | 0.041575 |
2 | 0.42216 | 0.476927 |
3 | 0.424337 | 0.369148 |
4 | 0.411378 | 0.131149 |
5 | 0.469893 | 0.131009 |
6 | 0.455647 | 0.056521 |
7 | 0.443464 | 0.000584 |
8 | 0.454903 | 0.151529 |
9 | 0.463397 | 0.343016 |
10 | 0.486252 | 0.103636 |
Average | 0.444524 | 0.180509 |
No | Target value (°) | Reached value (°) | Error (°) |
|---|---|---|---|
1 | 30 | 34.06459 | 4.064586 |
2 | 60 | 58.69824 | 1.301763 |
3 | 90 | 96.6034 | 6.603395 |
4 | 120 | 125.7604 | 5.760367 |
5 | 150 | 150.6944 | 0.694423 |
6 | 180 | 178.3868 | 1.61317 |
7 | 210 | 216.9049 | 6.904861 |
8 | 240 | 239.9423 | 0.057667 |
9 | 270 | 268.2965 | 1.703503 |
10 | 300 | 305.5362 | 5.536204 |
Average | - | - | 3.423994 |
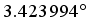 , which is the result of the control by the omnidirectional mobile robot using the proposed algorithm for different target orientation angles.
, which is the result of the control by the omnidirectional mobile robot using the proposed algorithm for different target orientation angles. AI | Artificial Intelligence |
RL | Reinforcement Learning |
DRL | Deep Reinforcement Learning |
DDPG | Deep Deterministic Policy Gradient |
UVFM | Univector Field Method |
APFM | Artificial Potential Field Method |
DQN | Deep Q-Network |
OMR | Omnidirectional Mobile Robot |
| [1] | Ashleigh S, Silvia F. A Cell Decomposition Approach to Cooperative Path Planning and Collision Avoidance via Disjunctive Programming. 49th IEEE Conference on Decision and Control; 2010 Dec 15-17; Atlanta, USA; 2011. 6329-8p. |
| [2] | Christoph Oberndorfer. Research on new Artificial Intelligence based Path Planning Algorithms with Focus on Autonomous Driving [PhM Thesis]. Munich: University of Applied Sciences Munich; 2017. |
| [3] | Koren Y, Borenstein J. Potential Field Methods and Their Inherent Limitations for Mobile Robot Navigation. Proceedings of the IEEE Conference on Robotics and Automation; 1991 Apr 7-12; California, USA; 1991. 1398-6p. |
| [4] | Arora T, Gigras Y, Arora V. Robotic Path Planning using Genetic Algorithm in Dynamic Environment. IJCA 2014; 89(11): 8-5p. |
| [5] | Mahadevi S, Shylaja KR, Ravinandan ME. Memory Based A-Star Algorithm for Path Planning of a Mobile Robot. IJSR 2014; 3(6): 1351-5p. |
| [6] | Yu ZN, Duan P, Meng LL, et al. Multi-objective path planning for mobile robot with an improved artificial bee colony algorithm. MBE 2022; 20(2): 2501-9p. |
| [7] | Ren Y, Liu JY. Automatic Obstacle Avoidance Path Planning Method for Unmanned Ground Vehicle Based on Improved Bee Colony Algorithm. JJMIE 2022; 16(1): 11-8p. |
| [8] | Sat C, Dayal RP. Navigational control strategy of humanoid robots using average fuzzy-neuro-genetic hybrid technique. IRAJ 2022; 8(1): 22-4p. |
| [9] | Jeevan R, Srihari PV, Satya JP, et al. Real Time Path Planning of Robot using Deep Reinforcement Learning. Preprints of the 21st IFAC World Congress (Virtual); July 12-17, 2020; Berlin, Germany; 2020. 15811-6p. |
| [10] | Shi YM, Zhang ZY. Research on Path Planning Strategy of Rescue Robot Based on Reinforcement Learning. Journal of Computers 2022; 33(3): 187-8p. |
| [11] | Lucia L, Daniel D, Gianluca C, et al. Robot Navigation in Crowded Environments Using Deep Reinforcement Learning. 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)(Virtual); October 25-29, 2020, Las Vegas, NV, USA; 2020. 5671-7p. |
| [12] | Phalgun C, Rolf D, Thomas H. Robotic Path Planning by Q Learning and a Performance Comparison with Classical Path Finding Algorithms. IJMERR 2022; 11(6): 373-6p. |
| [13] | Yang Y, Li JT, Peng LL. Multi-robot path planning based on a deep reinforcement learning DQN algorithm. CAAI Trans. Intell. Technol 2020; 5(3): 177-7p. |
| [14] | Zhu AY, Dai TH, Xu GY, et al. Deep Reinforcement Learning for Real-Time Assembly Planning in Robot-Based Prefabricated Construction. IEEE Trans. Auto. Sci. Technol 2023; 20(3): 1515-12p. |
| [15] | Chen Jiong. Construction of an Intelligent Robot Path Recognition System Supported by Deep Learning Network algorithms. IJACSA 2023; 14(10): 172-10p. |
| [16] | Yun JY, Ro KS, Pak JS, et al. Path Planning using DDPG Algorithm and Univector Field Method for Intelligent Mobile Robot. IJARAT 2024; 2(2): 7-11p. |
APA Style
Jin, K. K., Yon, Y. J., Song, R. K., Bin, J. K., Rim, P. M. (2025). Pose Control of Omnidirectional Mobile Robot Using Improved Deep Reinforcement Learning. International Journal of Industrial and Manufacturing Systems Engineering, 10(2), 36-43. https://doi.org/10.11648/j.ijimse.20251002.12
ACS Style
Jin, K. K.; Yon, Y. J.; Song, R. K.; Bin, J. K.; Rim, P. M. Pose Control of Omnidirectional Mobile Robot Using Improved Deep Reinforcement Learning. Int. J. Ind. Manuf. Syst. Eng. 2025, 10(2), 36-43. doi: 10.11648/j.ijimse.20251002.12
@article{10.11648/j.ijimse.20251002.12,
author = {Kim Kwang Jin and Yun Ji Yon and Ro Kang Song and Jo Kwang Bin and Pak Mu Rim},
title = {Pose Control of Omnidirectional Mobile Robot Using Improved Deep Reinforcement Learning
},
journal = {International Journal of Industrial and Manufacturing Systems Engineering},
volume = {10},
number = {2},
pages = {36-43},
doi = {10.11648/j.ijimse.20251002.12},
url = {https://doi.org/10.11648/j.ijimse.20251002.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijimse.20251002.12},
abstract = {Nowadays, mobile robots are being widely applied in various fields such as indoor carrying and check of products and outdoor exploration. One of the most important problems arising in development of mobile robots is to resolve path planning problem. With active studies of implementation of path planning, lots of algorithms have been developed and especially, the dramatic advance in artificial intelligence (AI) led to advent of algorithms using reinforcement learning (RL). Deep reinforcement learning (DRL) has been developed and it uses neural network to approximate parameters of RL algorithm. DDPG is one of deep reinforcement learning (RL) algorithms and is widely used to solve lots of practical issues as it doesn’t need full information of the environment. In other words, path planning with DRL has advantages of possibility for unknown environments in which partial or full information is not given and of direct controllability of the robot. Generally, path planning Up to now, path planning using DRL has considered only position control problem with no consideration of its orientation angle (as the author knows). In this paper, a pose control method using DRL for 3-wheeled omnidirectional mobile robot is proposed. And a method to reduce position error is mentioned. Simulation results show that the proposed method can efficiently solve the control problem of omnidirectional robots.
},
year = {2025}
}
TY - JOUR T1 - Pose Control of Omnidirectional Mobile Robot Using Improved Deep Reinforcement Learning AU - Kim Kwang Jin AU - Yun Ji Yon AU - Ro Kang Song AU - Jo Kwang Bin AU - Pak Mu Rim Y1 - 2025/10/09 PY - 2025 N1 - https://doi.org/10.11648/j.ijimse.20251002.12 DO - 10.11648/j.ijimse.20251002.12 T2 - International Journal of Industrial and Manufacturing Systems Engineering JF - International Journal of Industrial and Manufacturing Systems Engineering JO - International Journal of Industrial and Manufacturing Systems Engineering SP - 36 EP - 43 PB - Science Publishing Group SN - 2575-3142 UR - https://doi.org/10.11648/j.ijimse.20251002.12 AB - Nowadays, mobile robots are being widely applied in various fields such as indoor carrying and check of products and outdoor exploration. One of the most important problems arising in development of mobile robots is to resolve path planning problem. With active studies of implementation of path planning, lots of algorithms have been developed and especially, the dramatic advance in artificial intelligence (AI) led to advent of algorithms using reinforcement learning (RL). Deep reinforcement learning (DRL) has been developed and it uses neural network to approximate parameters of RL algorithm. DDPG is one of deep reinforcement learning (RL) algorithms and is widely used to solve lots of practical issues as it doesn’t need full information of the environment. In other words, path planning with DRL has advantages of possibility for unknown environments in which partial or full information is not given and of direct controllability of the robot. Generally, path planning Up to now, path planning using DRL has considered only position control problem with no consideration of its orientation angle (as the author knows). In this paper, a pose control method using DRL for 3-wheeled omnidirectional mobile robot is proposed. And a method to reduce position error is mentioned. Simulation results show that the proposed method can efficiently solve the control problem of omnidirectional robots. VL - 10 IS - 2 ER -